Redacción/Irene Vega
Físicos del Grupo de Dinámica No Lineal, Teoría del Caos y Sistemas Complejos de la Universidad Rey Juan Carlos, que dirige el catedrático de Física Miguel A.F. Sanjuán, han desarrollado un nuevo y novedoso método para determinar si un sistema dinámico posee la propiedad de Wada, que afecta a nuestra capacidad de predicción del modelo físico. Desde sencillos péndulos a modelos de dinámica galáctica o sistemas ecológicos muestran esta propiedad topológica. El estudio ha sido recientemente publicado en la prestigiosa revista Communications in Nonlinear Science and Numerical Simulations, una de las de mayor índice de impacto en Dinámica No Lineal.
Como ejemplo de aplicación del método de saddle-straddle, los investigadores de la URJC emplearon el péndulo amortiguado y forzado, un sistema paradigmático en Dinámica No Lineal que presenta la propiedad de Wada para ciertos valores de sus parámetros. Este método hace uso de la silla caótica, un conjunto fractal que vive en la frontera de las cuencas de Wada y que es el responsable de la extrema sensibilidad del sistema. “La observación clave del presente método es que en sistemas con la propiedad de Wada la silla caótica no cambia cuando se calcula para diferentes pares de cuencas”, afirma Miguel A.F. Sanjuán.
Las cuencas de Wada son regiones de atracción fractales que dificultan la predicción del comportamiento de algunos sistemas dinámicos caóticos. Desde el punto de vista práctico, para probar la propiedad de Wada todo lo que hay que hacer es tener tres o más cuencas fractales en el espacio de fases, y demostrar numéricamente que solo hay una silla caótica. “Si podemos demostrar que el conjunto de puntos que conforman la silla caótica es el mismo para todos los pares de cuencas fusionadas, tendríamos éxito en demostrar que solo hay una silla caótica y, en consecuencia, que las cuencas son Wada”, explica Alexandre Wagemakers, investigador de la URJC.
Para la aplicación de este método es importante conocer el número de atractores que intervienen. Un atractor es un conjunto de valores numéricos hacia los cuales un sistema tiende a evolucionar, dada una gran variedad de condiciones iniciales en el sistema. El algoritmo saddle-straddle se encarga de calcular la silla caótica en la frontera que separa al menos dos cuencas. “Sin embargo, no necesitamos calcular las cuencas de atracción, ya que basta conocer un conjunto de condiciones iniciales que conduzcan a estos atractores”, apunta Alexandre Wagemakers. “Esto supone una ventaja frente a otros métodos previos”.
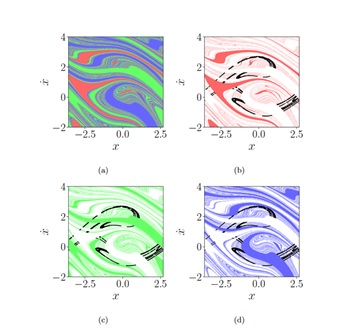
La idea del proceso se ilustra en la figura. El panel (a) muestra las tres cuencas de atracción de este sistema con la propiedad de Wada, lo cual indica que hay tres atractores cuyas cuencas comparten una misma frontera. Las figuras (b), (c) y (d) muestran cada una de las cuencas con su respectivo color, y las otras dos están fusionadas y aparecen en color blanco. Los puntos negros son puntos de la silla caótica. Una simple inspección visual sugiere que las sillas caóticas calculadas de este modo son las mismas, lo que inmediatamente nos llevaría a concluir que el sistema tiene la propiedad de Wada. “Sin embargo, comparar conjuntos fractales no es algo sencillo”, explica Álvar Daza, coautor del estudio. “Para comparar entre sí las sillas correspondientes a las diferentes cuencas es necesario realizar un cálculo de las distancias de Hausdorff entre los diferentes conjuntos de puntos”. Para un elevando número de puntos, el cálculo de esta distancia es pequeño y similar entre los diferentes conjuntos, lo que confirma que los puntos pertenecen en realidad a la misma silla caótica y, por lo tanto, el sistema posee la propiedad de Wada.