Redacción/ Irene Vega
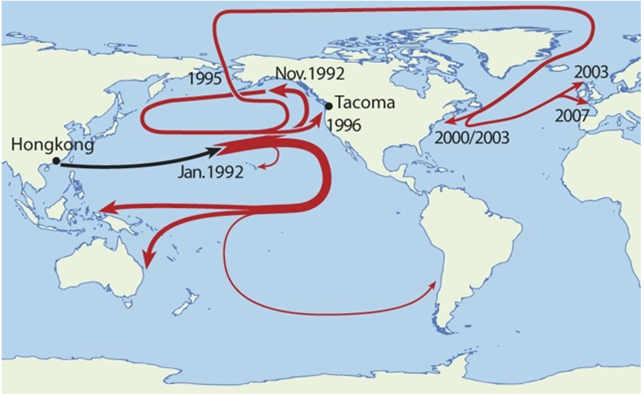
En 1992, un carguero que cubría la ruta entre Hong Kong y Tacoma perdió 12 contenedores durante una tormenta. Uno de esos contenedores contenía un ejército de 29.000 patitos de plástico que quedaron a la deriva en el medio del océano. Diez meses después, algunos de estos juguetes aparecieron en las costas de Alaska, a 3200 km del lugar del incidente. Pasaron los meses y nuevas hordas de curtidos patitos fueron apareciendo en lugares tan variopintos como Australia, Indonesia, Chile o Hawái. Es más, algunos de los patos que aún seguían a la deriva, lograron colarse por el estrecho de Bering y 10 años después de empezar su aventura, aparecían en lugares tan remotos como Islandia.
Este suceso representa un excelente ejemplo de lo que es una dinámica caótica con escapes. Las corrientes oceánicas forman una intrincada red de transporte a través de las cuales viajan todo tipo de objetos flotantes. Aunque en un primer momento estos objetos inicien su deriva desde el mismo punto del océano, la acción de las corrientes va progresivamente separando sus trayectorias. Incluso la más pequeña diferencia en la posición inicial, o cualquier mínima fluctuación en las fuerzas que actúan sobre ellos, hace que en algún momento sus caminos se separen y que eventualmente terminen su viaje (escape) en lugares totalmente diferentes.
Trayectorias seguidas por los patitos desde 1992
¿Y si fuera posible controlar tanto el destino como la hora de llegada de uno de estos objetos flotantes? Un problema de características similares es lo que los físicos del Grupo de Dinámica No Lineal, Teoría del Caos y Sistemas Complejos de la Universidad Rey Juan Carlos, que dirige el catedrático de Física Miguel A.F. Sanjuán, han investigado, cuyos resultados han sido publicados recientemente en la prestigiosa revista Nonlinear Dynamics.
El estudio se centra en la bien conocida aplicación logística, propuesta originalmente por el físico Lord Robert May de la Universidad de Oxford para el estudio del comportamiento dinámico de la población de una especie. Esta aplicación solo contiene un parámetro r, y en función de su valor se pueden encontrar diferentes comportamientos dinámicos. Uno de los más interesantes aparece para valores de r>4 donde el sistema presenta una dinámica caótica con escapes. En este régimen la población de la especie fluctúa de forma irregular durante un tiempo para finalmente escapar hacia un comportamiento dinámico distinto. “Debido a la no linealidad del sistema y al ruido que le afecta, este escape se produce de forma impredecible. No es posible conocer de antemano cuándo sucederá”, señala Gaspar Alfaro.
Con el objetivo de controlar cuándo se produce este escape, el trabajo contempla dos alternativas. En la primera de ellas, se perturba el sistema caótico de tal forma que el escape se produzca antes de un tiempo límite, previamente determinado por el controlador. En la segunda, el objetivo es más específico. En ella el sistema se perturba para que el escape tenga lugar en un instante determinado, previamente indicado por el controlador. “Aplicando pequeñas perturbaciones al sistema, conseguimos modificar su comportamiento para que tanto el escape como el momento en que se produce puedan ser controlados a voluntad. Además, el método que proponemos contempla la presencia de fluctuaciones externas (ruido afectando el sistema) para que su aplicación sea más realista”, apunta Rubén Capeáns.
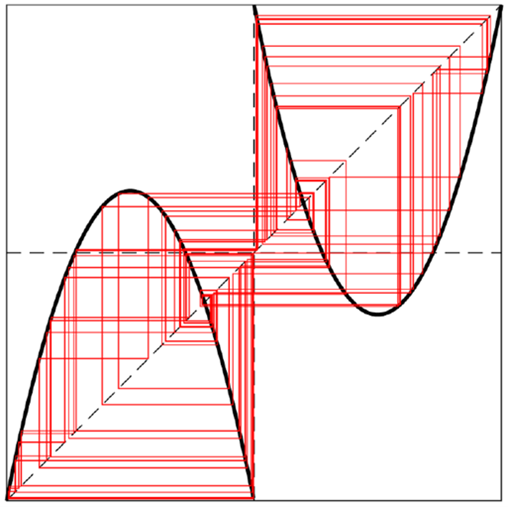
En este estudio, además, se propone una nueva aplicación caótica compuesta de dos regiones A y B tal como se muestra en la figura. En ausencia de control, las trayectorias que inicialmente se encuentran en la región A pueden migrar (escapar) hacia la región B o también escapar a una región exterior. Dado que la dinámica de esta aplicación es caótica y está a su vez afectada por ruido, la evolución del sistema resulta impredecible. “Sin embargo, nuestro trabajo muestra que es posible controlar las trayectorias de este sistema de forma que su movimiento quede restringido a las regiones A y B, y lo que es más sorprendente, el tiempo que éstas permanecen en cada una de estas dos regiones”, señala Gaspar Alfaro.
Sistema dinámico discreto con dos regiones caóticas
Finalmente, “aunque el sistema dinámico que hemos usado es de una sola dimensión, este método de control es fácilmente extrapolable a sistemas de dimensión mayor. Con su aplicación, los escapes caóticos propios de sistemas no lineales dejan de ser impredecibles”, concluye Miguel A.F. Sanjuán.