Redacción/Irene Vega
Los investigadores del Grupo de Dinámica No Lineal, Teoría del Caos y Sistemas Complejos de la Universidad Rey Juan Carlos, que dirige el catedrático de Física Miguel A.F. Sanjuán, han caracterizado recientemente un nuevo fenómeno de resonancia que se produce en los modelos de osciladores no lineales con retardo, conocido como resonancia inducida por retardo. Mediante este interesante fenómeno se puede aumentar las amplitudes de las oscilaciones de un sistema gracias a la interacción entre el forzamiento externo y el término de retardo. La utilización de modelos que incluyen un retardo se hace necesaria ya que, en la naturaleza, la trasmisión de información nunca es instantánea.
En colaboración con el profesor S. Rajasekar del Centre for Nonlinear Dynamics de la Bharathidasan University de la India, el equipo científico de la URJC ha publicado un nuevo trabajo, empleando los resultados obtenidos anteriormente. Los investigadores del grupo han demostrado cómo este fenómeno de resonancia puede contrarrestar la impredecibilidad de un sistema generada por efecto del amortiguamiento. “Hay que tener en cuenta que la impredecibilidad es una propiedad de los sistemas caóticos que a menudo se quiere suprimir o, por los menos, disminuir. La posibilidad de predicción de las dinámicas de un sistema puede ser interesante en multitud de campos cómo la neurociencia, la meteorología, la electrónica, las telecomunicaciones, la economía entre muchos otros. En todos estos campos se emplean a menudo modelos que incluyen un retardo, y en todos ellos el amortiguamiento puede jugar un papel importante introduciendo impredecibilidad en las dinámicas de los sistemas estudiados”, señala Miguel A.F. Sanjuán.
El trabajo, publicado en la revista Philosohical Transactions of the Royal Society A, forma parte como publicación invitada de un número especial sobre el fenómeno de la resonancia en sistemas no lineales. La Philosohical Transactions of the Royal Society A es la revista científica más antigua en inglés, además de ser una referencia en el campo de la física.
Cómo se contrarresta la impredecibilidad de un sistema generada por efecto del amortiguamiento
Como modelo de estudio, los investigadores de la URJC eligieron un oscilador no lineal clásico con amortiguamiento, el oscilador de Duffing, que posee un potencial de doble pozo, biestable y con una región de parámetros para los cuales el movimiento es caótico. Lo primero que se notó fue lo que se ve en la figura (a). “Es interesante analizar las cuencas de amplitud en función del término de retardo τ frente al amortiguamiento µ. Este tipo de graficas nos permiten, gracias a un mapa de colores, conocer el valor de la amplitud de las oscilaciones conocidos un par de parámetros del sistema. De este modo, en la figura (a) vemos que cuánto más crezca el parámetro µ, más se mezclan estas cuencas entre ellas adquiriendo un carácter fractal, y aumentando, por ende, la impredecibilidad del sistema”, explica Miguel A.F. Sanjuán.
Continuando con la explicación de la figura (a), el profesor Jesús M. Seoane puntualiza: “Hay que tener en cuenta que sólo por algunos valores del término de retardo las cuencas asumen propiedades fractales, para los demás valores estudiados las cuencas de amplitud no se ven afectadas por el amortiguamiento”.
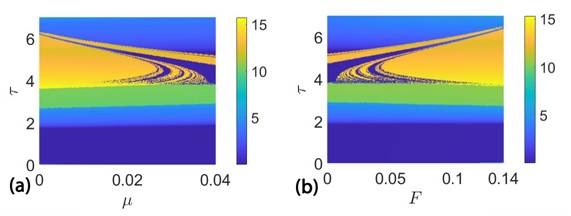
En la figura (b), la investigadora Julia Cantisán señala que “por otro lado la introducción de un forzamiento externo, y con él la generación de la resonancia inducida por retardo, permite la restauración de las cuencas de amplitud que se encuentran cuando no hay amortiguamiento”.
En ambas figuras se puede observar que los dos efectos se confrontan. En la figura (a) se ve cómo las cuencas de amplitud, calculadas sin forzamiento, pierden cohesión a medida que aumenta el parámetro µ. Mientras, que en la figura (b) se puede apreciar la recomposición de las cuencas de amplitud, calculadas para un valor fijo del amortiguamiento µ=0.04, a medida que aumenta el forzamiento externo F.
“El hecho de que las oscilaciones se vean restauradas por la resonancia es un hecho relevante por lo que se estudia en profundidad en el presente trabajo. Es de resaltar el hecho que, en ausencia de amortiguamiento, se reestablecen tanto las amplitudes como las frecuencias originales. Es decir, para un cierto valor del forzamiento externo se obtienen las mismas oscilaciones que había antes de introducir el amortiguamiento”, explica Mattia Coccolo.
Los investigadores han demostrado que es posible contrarrestar los efectos de impredecibilidad introducidos por el amortiguamiento con la introducción de un forzamiento que genere la resonancia inducida por retardo. Además, es también posible recuperar las oscilaciones del sistema a la situación original en la que no había amortiguamiento.
